Classification
Binary Classification
Binary classification tasks are problems with target values that fall under two categories: one positive class, one negative class. For example, in a churn prediction problem, you want to predict whether a customer leaves your service in the near future, so the labels can be defined as:
- Positive Class: the customer discontinues your service.
- Negative Class: the customer continues your service.
Whenever you write a predictive query with a target that contains a conditional operation such as =, > or <, the task will be defined as a binary classification task.
The prediction output for a binary classification task is the probability that the target value belongs to the positive class. A classification threshold determines how high the predicted probability must be for it to be considered a positive class prediction. Kumo uses accuracy, AUROC, and AUPRC as the evaluation metrics for this task, and provides a confusion matrix and a cumulative gain chart to help understand the results.
Accuracy
The accuracy tells you the overall percentage of correct predictions. The accuracy score is given by the total number of correct predictions over the number of samples.
AUROC
The AUROC stands for the area under the receiver operating characteristic curve, which is a curve plotting sensitivity against specificity under different classification thresholds.
Sensitivity is calculated by:
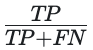
where TP (number of true positives) counts customers who stop purchasing and the model correctly predicts this behavior and FN (number of false negatives) counts customers who stop purchasing with us but the model predicts they'd continue.
Specificity is calculated by:
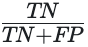
where TN (number of true negatives) counts customers who continue purchasing and the model predicted correctly this behavior, and FP (number of false positives) counts customers who continue purchasing but the model predicted they'd leave.
A perfect predictor yields an AUROC score of 1, a predictor that makes completely random predictions yields an AUROC score of 0.5. An AUROC of 0.8 is typically considered very good, but what is considered good enough will depend on your specific business problem.
AUPRC
The AUPRC stands for the area under the precision-recall curve, which is a curve plotting precision against recall under different classification thresholds.
Precision is calculated by:
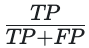
where FP (number of false positives) counts customers who continue purchasing with us but the model predicts they stop.
Recall is calculated by:
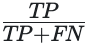
A perfect predictor yields an AUPRC score of 1. The baseline for determining what makes a better-than-random AUPRC score is different for each problem - specifically, it depends on how imbalanced the data is. For example, if your problem has 10% positive class and 90% negative class, then a predictor that always arbitrarily makes positive predictions would achieve an AUPRC of 0.1.
AUPRC is typically considered a better metric when you have imbalanced data (e.g., you are trying to make good predictions for a very rare class), since it is much more sensitive to changes in performance for predicting that rare class. On the other hand, with a metric like accuracy, you could achieve very high metrics by just predicting that a rare positive class never happens.
Depending on your business focus, changing the threshold above which predictions are considered positive will change accuracy, specificity, sensitivity, precision, and recall scores, but a single AUROC or AUPRC score captures how good the overall performance is under different thresholds.
Confusion Matrix
Kumo provides a confusion matrix that presents the number of true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) on the same graph. The confusion matrix can be read as follows:
| Predicted Negative Class | Predicted Positive Class | |
|---|---|---|
| Actual negative class | TN | FP |
| Actual positive class | FN | TP |
A good model will generally have significantly higher values in the TN and TP boxes compared to the FN and FP boxes. But you should always consider what these four values mean in the scope of your business problem.
Cumulative Gain Chart
The cumulative gain chart shows the percentage of "gain" you can achieve in a certain class by taking a particular action. For example, suppose that the graph below is the result of a churn prediction query:
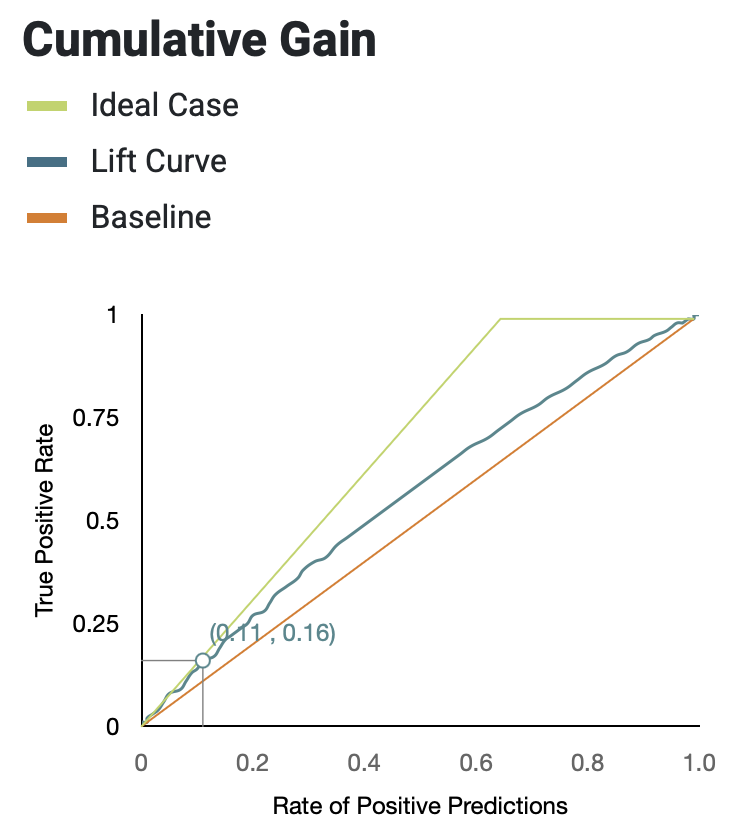
The (0.11, 0.16) datapoint translates to the following: if you reach out to 11% (the action) of all customers, you will find 16% (the "gain") of all customers who will leave in the near future. The better your model, the smaller the percentage of customers you'll need to reach out to in order to net a disproportionately larger share of the customers likely to churn.
A gain chart plots the TP rate against the rate of positive predictions. The TP rate is given by:
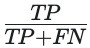
and the rate of positive predictions is given by:
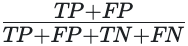
The result of a random model is used as the baseline, shown by the straight orange line.
Kumo defines an ideal model as one that is always correct when it makes a positive class prediction, shown by the green curve in the previous graph. The blue curve in between shows the actual model performance. Qualitatively, a better model will have a larger area between the blue and orange curves; the two numbers shown on the graph also convey a powerful message.
Multiclass Classification
Kumo uses the accuracy score as the metric in a multiclass classification problem. The accuracy score presents the percentage of correct class prediction, and is given by the total number of correct class predictions over the number of samples.
Multilabel Classification
For a multilabel classification problem, Kumo calculates the same precision and recall score for each class as in the binary classification case. You can also look at the F1 score, which takes both precision and recall into consideration, calculated by:
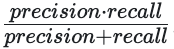
Kumo also provides the Hamming score as a measure of accuracy across multiple classes. The Hamming score is calculated by:
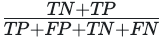
which translates to the percentage of correct predictions over all predictions.
Updated 2 months ago
